เมทริกซ์

00:35:00 THE MATHRIC Q&A 0 Comments


เมทริกซ์
การเขียนเมทริกซ์
             เป็นชุดตัวเลขที่อยู่ภายในเครื่องหมาย [ ] รือ ( ) ซึ่งมีการจัดเรียงในแนวนอนหรือแนวแถว และแนวตั้งหรือ สดมภ์ 
แนวตั้งหรือสดมภ์ แนวนอน  หรือ แนวแถว
                                      



ตัวอย่าง 1  เป็นตัวอย่างของเมทริกซ์ที่มี 3 แถวและ 2 สดมภ์ 
                                                      
                                                                                                          2 สดมภ์
3 แถว

                                                                                                                                    หรือ

                           โดยมีตัวเลขที่เรียงในแถวที่ 1 คือ 1 2
                                                           แถวที่ 2 คือ 3 4
                                                           แถวที่ 3 คือ 5 6

               สมาชิก  
              เป็นตัวเลขที่อยู่ภายในเมทริกซ์จากตัวอย่าง 9.1 สมาชิกมีเลข 1 2 3 4 5 6 คือ
         สมาชิก
      
                                                              


               มิติ
             เป็นตัวเลขที่แสดงถึงจำนวนแถว คูณจำนวนสดมภ์ จากตัวอย่าง 9.1 มิติเป็น 3x2
  3 x 2 มิติ
               ขนาด
            เป็นผลคูณของจำนวนแถวกับจำนวนสดมภ์ จากตัวอย่าง 9.1 ขนาดเป็น 6
                                                 
3x2  ผลคูณ = 6

               การตั้งชื่อ 
            การตั้งชื่อของเมทริกซ์และสมาชิก
           ก. การตั้งชื่อของเมทริกซ์  
                    จะใช้อักษรภาษาอังกฤษตัวใหญ่ เช่น A, B, C, ... เมื่อตั้งชื่อเมทริกซ์แล้วจะตามด้วยเครื่องหมาย '=' และ
เมทริกซ์ที่ประกอบด้วยสมาชิกจากตัวอย่าง 9.1 อาจตั้งชื่อเมทริกซ์เป็น A  ดังนี้

A =   หรือ A  =

          ซึ่ง A เป็นชื่อของเมทริกซ์และตามด้วยเครื่องหมาย "=" ที่ประกอบด้วย สมาชิก 1 2 3 4 5 6
          

          ข.  การตั้งชื่อสมาชิก 
                    จะใช้อักษรภาษาอังกฤษตัวเล็ก พร้อมทั้งระบุตำแหน่งแถวและสดมภ์กำกับเป็นตัวห้อย
เช่น a12  หมายถึง สมาชิกที่อยู่ในตำแหน่งแถวที่ 1 และ   สดมภ์ที่ 2 สำหรับอักษร a จะใช้ชื่อให้สอดคล้องกับชื่อของเมทริกซ์
                             คือถ้าชื่อเมทริกซ์เป็น A จะตั้งชื่อของเมทริกซ์เป็น a 

                                                       
             ดังนั้นเมทริกซ์ใดๆ สามารถเขียนเป็นรูปทั่วไปดังนี้
      A = 
                                           

            เมื่อ A มีมิติเป็น m x n
                                  โดยมี  a11 อยู่ในแถวที่ 1  และสดมภ์ที่ 1
                                            a12 อยู่ในแถวที่ 1  และสดมภ์ที่ 2   
                                                                        :  
                                           amn อยู่ในแถวที่ m และสดมภ์ที่ n
เมทริกซ์จัตุรัส
            เป็นเมทริกซ์ที่มีจำนวนแถวและจำนวนสดมภ์เท่ากัน
                                                                   
          เช่น
                    
A  =  เป็นเมทริกซ์จัตุรัสมิติ 2x2 ที่มีจำนวนแถว 2 แถวและจำนวนสดมภ์ 2 สดมภ์

    B  =  เป็นเมทริกซ์จัตุรัสมิติ 3x3 ที่มีจำนวนแถว 3 แถวและจำนวนสดมภ์ 3 สดมภ์
                    

               เมทริกซ์เอกลักษณ์
         เป็นเมทริกซ์จัตุรัสที่สมาชิกในตำแหน่งแถวเท่ากับตำแหน่งสดมภ์จะมีสมาชิกมีค่าเป็น   1 และในทางกลับกันสมาชิก
ในตำแหน่งแถวไม่เท่ากับตำแหน่งสดมภ์ จะมีสมาชิกมีค่าเป็น 0



ตัวอย่าง 2  เป็นตัวอย่างของเมทริกซ์เอกลักษณ์มิติ 2x2 
             เป็นเมทริกซ์เอกลักษณ์มิติ 2x2  ตำแหน่งแถวเท่ากับตำแหน่งสดมภ์ มีสมาชิกในตำแหน่งแถวที่ 1 สดมภ์ที่ 1
และสมาชิกที่อยู่ตำแหน่งแถวที่ 2 สดมภ์ที่ 2 มีค่าสมาชิกเป็น  1  ตำแหน่งแถวไม่เท่ากับตำแหน่งสดมภ์  สมาชิกที่อยู่
ในตำแหน่งแถวที่ 1 สดมภ์ที่ 2 และ สมาชิกที่อยู่ในตำแหน่งแถวที่ 2  สดมภ์ที่ 1 มีค่าเป็น  0

ตัวอย่าง 3  แสดงเมทริกซ์เอกลักษณ์มิติ 3x3
B  =  

              B เป็นเมทริกซ์เอกลักษณ์มิติ 3x3  ที่มีสมาชิกที่อยู่ในตำแหน่งแถวที่ 1 สดมภ์ที่ 1, ตำแหน่งแถวที่ 2 สดมภ์ที่ 2
และ ตำแหน่งแถวที่ 3 สดมภ์ที่ 3 เป็น 1 เพราะตำแหน่งแถวเท่ากับตำแหน่งสดมภ์  ที่เหลือของสมาชิกมีค่าเป็น 0
เพราะตำแหน่งแถวไม่เท่ากับตำแหน่งสดมภ์

              ดังนั้นสามารถเขียนสมาชิกของเมทริกซ์เอกลักษณ์เป็นรูปทั่วไปได้ดังนี้
aij =
     , i เท่ากับ j
     , i ไม่เท่ากับ j
             เมื่อ  i    เป็นตำแหน่งแถว และ  j เป็นตำแหน่งสดมภ์
                  aij   เป็นสมาชิกของตำแหน่งแถวที่ i  และตำแหน่งสดมภ์ที่ j

               เมทริกซ์ศูนย์
            เป็นเมทริกซ์ที่มีสมาชิกทุกตัวเป็นศูนย์

ตัวอย่าง 4  แสดงเมทริกซ์ที่มีสมาชิกเป็นศูนย์ทั้งที่เป็นไม่ใช่เมทริกซ์จัตุรัสและเมทริกซ์จัตุรัส
 

                                                                   

             จะเห็นว่าเมทริกซ์ทางซ้าย  ตอนกลาง  เป็นเมทริกซ์ที่ไม่ใช่จัตุรัส แต่ที่สมาชิกเป็นศูนย์  ส่วนเมทริกซ์ขวาสุด
เป็นเมทริกซ์จัตุรัส ที่มีสมาชิกทุกตัวเป็นศูนย์

               เมทริกซ์ทแยงมุม
             เป็นเมทริกซ์จัตุรัสที่มีสมาชิกที่อยู่เหนือและใต้ทแยงมุมเป็นศูนย์

ตัวอย่าง 5  แสดงเมทริกซ์ทแยงมุมที่มีมิติ 2x2, 3x3

                                                

ข้อสังเกต สมาชิกที่อยู่ในแนวทแยงมุมมีค่าไม่เท่ากัน แต่สมาชิกที่อยู่เหนือหรือใต้เส้นทแยงมุมเป็นศูนย์

               เมทริกซ์สเกลาร์
              เป็นเมทริกซ์จัตุรัส ที่มีสมาชิกที่อยู่ในแนวทแยงมุมเท่ากัน และสมาชิกที่อยู่เหนือ, ใต้ทแยงมุมเป็นศูนย์

ตัวอย่าง 6  แสดงเมทริกซ์สเกลาร์มิติ 2x2, 3x3 

                                                

            จะเห็นว่าสมาชิกในแนวทแยงมีค่าเท่ากันแต่สมาชิกที่อยู่เหนือทแยงมุมและใต้ทแยงมุมเป็นศูนย์ 

               เมทริกซ์สลับเปลี่ยน
            เป็นเมทริกซ์ที่มีสมาชิกที่อยู่ในแนวแถวมาจากสมาชิกในแนวสดมภ์หรือสมาชิกที่อยู่ในแนวสมาชิกที่อยู่ในแนวสดมภ์
เป็นสมาชิกในแนวแถว
                                            ซึ่งมีสัญลักษณ์ เป็น AT หรือ At

ตัวอย่าง 7  ให้ A เป็นเมทริกซ์มิติ 2x2 และ B เป็นเมทริกซ์มิติ 2x3 

 
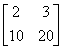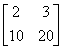   A =   ,   B = 
                                                                            2 x 2                               2 x 3


จงหาเมทริกซ์สลับเปลี่ยน  AT, BT
วิธีทำ
    AT   =         ,  BT = 
                                                                               2 x 2                         3 x 2
ข้อสังเกตุ มิติของเมทริกซ์สลับเปลี่ยน จะสลับที่กับมิติของเมทริกซ์เดิม


               การบวกลบเมทริกซ์
             ในการที่เมทริกซ์ตั้งแต่ 2 เมทริกซ์ขึ้นไปจะนำมาบวกลบกันได้จะต้องมีมิติเดียวกัน หลังจากนั้นให้นำสมาชิกที่อยู่ใน
ตำแหน่งแถว และตำแหน่งสดมภ์ตรงกันมาบวกลบกันได้ ผลลัพธ์ที่ได้ใส่ไว้ที่ตำแหน่งแถว    และสดมภ์นั้นของเมทริกซ์ที่เก็บ
ผลลัพธ์ของการบวกและลบ ซึ่งจะมีมิติเท่ากับมิติของเมทริกซ์ที่นำ
มาบวก ลบกัน


ตัวอย่าง 8   แสดงถึงเมทริกซ์ใดที่สามารถบวก ลบกันได้

               ให้    A =  [1 2 3]     
                       B =     
                      C =  [7 8 9]

            จะเห็นว่าเมทริกซ์ที่สามารถบวกลบกันได้นั้น มีเมทริกซ์ A กับ C เท่านั้นเพราะว่าเมทริกซ์ A กับ C มีมิติเดียวกัน
คือ 1x3 ซึ่งสัญลักษณ์สำหรับการบวก ลบ คือ + -
                    ดังนั้น
                                    A+C  =  [1 2 3] + [7 8 9]     
                                    A+C  =  [ 1+7  2+8  3+9 ]   สมาชิกที่อยู่ในตำแหน่งเดียวกัน สามารถ บวกกันได้เช่นสมาชิก 1, 7
                                                                                    อยู่ในตำแหน่งเดียวกันคืออยู่ที่แถวที่ 1   และสดมภ์ที่ 1
                                              =  [ 8     10     12 ]
                                     A-C  =  [1 2 3] - [7 8 9]  
                                     A-C  =  [ 1-7  2-8   3-9 ]     สมาชิกที่อยู่ในตำแหน่งเดียวกัน สามารถ   ลบกันได้
                                              =  [ -6    -6     -6 ]
            จากการบวกลบเมทริกซ์ สามารถเขียนเป็นรูปทั่วไปของการบวกลบได้ดังนี้
                             ให้ A = [aij] และ B = [bij] ที่เป็นเมทริกซ์มิติ mxn
                             แล้ว
                             ผลบวกของเมทริกซ์ A กับเมทริกซ์ B เป็น A+B ซึ่งมีค่าเป็น [aij + bij] มิติ mxn
                             ผลลบของเมทริกซ์  A  กับเมทริกซ์ B เป็น A-B ซึ่งมีค่าเป็น [aij - bij]  มิติ mxn

ตัวอย่าง 9 บริษัทแห่งหนึ่งมี 2 สาขา จำหน่ายอะไหล่รถจักรยานยนต์ เช่นหมวกกันน๊อค ซึ่งแต่ละสาขาได้แสดงข้อมูล
ของการจำหน่ายหมวกกันน๊อค เป็นจำนวนใบต่อวัน แยกตามสีและแบบ ดังนี้
                                     สาขาที่ 1
                                                                                       
                                  สาขาที่ 2
                                                  

             อยากทราบว่าจำหน่ายหมวกกันน๊อคทั้งหมดของทั้ง 2 สาขา แยกตาม  สีและแบบจำนวนกี่ใบ
วิธีทำ
                  จากข้อมูลสาขาที่ 1 แปลงเป็นเมทริกซ์ได้เป็น

 

                                และสาขาที่ 2 แปลงเป็นเมทริกซ์เป็น
  

                  ดังนั้น      
                      ทั้งสองเมทริกซ์ คำนวณหาค่าของผลรวมของเมทริกซ์ได้ดังนี้
                      
+ =
      
                      =
                        จากผลลัพธ์ที่ได้นำมาแปลงกลับเป็นตารางได้ดังนี้
                                          

การคูณเมทริกซ์
            มี 2 แบบคือ
            9.4.1 ตัวเลขคงที่ใดๆ หรือตัวอักษรที่เป็นค่าคงที่ คูณกับเมทริกซ์
            9.4.2 เมทริกซ์คูณกับเมทริกซ์

            9.4.1 ตัวเลขคงที่ใดๆ หรือตัวอักษรที่เป็นค่าคงที่ คูณกับเมทริกซ์
                       ให้นำค่าคงที่นั้นหรือตัวอักษรนั้นคูณเข้ากับสมาชิกทุกตัวของเมทริกซ์


ตัวอย่าง 2.10 ให้ A เป็นเมทริกซ์มิติ 1x3
                                     A = [ 1  2  3 ]
                           จงหาค่าของ 10A
วิธีทำ
                           10A = [ 1x10  2x10  3x10 ]   จะเห็นว่าสมาชิกทุกตัวถูกคูณด้วย 10
                                    = [ 10      20     30  ]   

ตัวอย่าง 2.11 พ่อค้าคนหนึ่งซื้อผลไม้มาขายเพียง 3 ชนิดคือ ส้ม มะม่วง และกล้วย ซึ่งได้แสดงต้นทุนคิดเป็นต่อ 1 กิโลกรัม
                          แสดงเป็นตาราง ดังนี้
                                                             
           พ่อค้าคนนี้ต้องการนำผลไม้เหล่านั้นไปขาย โดยมีความต้องการที่จะให้ได้กำไรกิโลกรัมละ 10% ของผลไม้ทุกชนิด
จงคำนวณหาราคาขายต่อกิโลกรัม
วิธีทำ
                      นำข้อมูลของตาราง แปลงเป็นเมทริกซ์

                     เมื่อต้องการกำไร 10% ราคาขายแสดงเป็นเมทริกซ์ได้ดังนี้
                                            
                                   

= 

                    ผลที่ได้นำมาแสดงเป็นตารางได้ดังนี้
                                        
               เมทริกซ์คูณกับเมทริกซ์
                          เมทริกซ์ที่จะคูณกันได้นั้นต้องตรวจดูมิติของเมทริกซ์ที่จะนำมาคูณก่อน กล่าวคือ เมทริกซ์ที่หนึ่งต้องมีมิติ ที่จำนวนสดมภ์เท่ากับจำนวนแถวของเมทริกซ์ที่สอง แล้วเมทริกซ์ที่เป็นผลลัพธ์จะมีมิติเป็นจำนวนแถว เท่ากับ จำนวนแถวของเมทริกซ์ที่หนึ่งและจำนวนสดมภ์เท่ากับจำนวนสดมภ์ของเมทริกซ์ที่สองหลังจากนั้นนำเมทริกซ์มาคูณกันได้โดยการนำสมาชิกแถวของเมทริกซ์ที่หนึ่งคูณกับสมาชิกที่อยู่ในสดมภ์ของเมทริกซ์ที่สองแล้วนำมารวมกัน ดังนั้นเขียนในรูปทั่วไป
สำหรับการคูณเมทริกซ์ได้ดังนี้

                                ให้ A =          เป็นเมทริกซ์มิติ 1xn              
        B  =  เป็นเมทริกซ์มิติ n x1ตัวอย่าง 12
         
                                  AB = ให้  A, B เป็นเมทริกซ์ 

                                        A = [1  2  3 ]  
                                        B  =                                         จงหา AB
วิธีทำ  A มีมิติ      1x3    ส่วน B มิติ     3x3
            ซึ่งจำนวนสดมภ์ของเมทริกซ์ A เท่ากับจำนวนแถวของเมทริกซ์ B ทำให้สามารถคูณกันได้

                 AB   = [1  2  3 ]1x3   
                  =                           =  [10+40+30   -1-4-9]
                           =   [ 80   -14]
จะเห็นว่าเมทริกซ์ A เป็นเมทริกซ์ที่มีมิติ 1x3   และ B เป็นเมทริกซ์ที่มีมิติเป็น 3x2 ซึ่งสามารถคูณกันได้เพราะจำนวนสดมภ์
ของเมทริกซ์ A เป็น 3 ซึ่งเท่ากับจำนวนแถวของเมทริกซ์ B ผลลัพธ์ของเมทริกซ์ใหม่มีมิติเป็น 1x2  สำหรับการคูณนั้นสมาชิก
ของแถวที่ 1 ของเมทริกซ์ A   คูณกับสดมภ์ที่ 1  ของเมทริกซ์ B  แล้ว นำผลลัพธ์ของการคูณรวมกัน  จะเป็นสมาชิกของ
เมทริกซ์ใหม่ที่อยู่ในตำแหน่งแถวที่ 1 และสดมภ์ที่ 1   สำหรับสมาชิกอื่นๆ จะทำทำนองเดียวกัน

ตัวอย่าง 9.13 ศูนย์กลางค้าแห่งหนึ่งได้จัดรายการสินค้า  เพื่อลดราคาของสองสาขา ซึ่งได้แสดงข้อมูลเป็นสองตาราง
คือตารางที่ 2.1 และ 2.2  ซึ่งแสดงไว้ที่ข้างล่างนี้  โดยตารางที่ 2.1      เป็นตารางแสดงราคาขายต่อหน่วยของสินค้า
แชมพู  สบู่  ยาย้อมผม   ส่วนตารางที่ 2.2   เป็นตารางแสดงจำนวนเงินที่ลดต่อหน่วยของสินค้า

                                    


ตารางที่ 9.1  แสดงราคาขายต่อหน่วยของสินค้าที่เป็นแชมพู สบู่ ยาย้อมผม
                                                          

                                               
ตารางที่ 9.2 แสดงจำนวนเงินที่ลดต่อหน่วยของสองสาขา
                                                            

              ศูนย์กลางค้านี้ต้องการที่จะทราบว่าจำนวนเงินที่ลดทั้งหมดของการขายสินค้า แชมพู สบู่ ยาย้อมผมต่อหน่วย
ของทั้งสองสาขาเป็นเท่าไร
               วิธีทำ

                      ข้อมูลของตารางที่ 9.1 แปลงเป็นเมทริกซ์ได้ดังนี้
                           
                       
                 ข้อมูลของตารางที่ 9.2 แปลงเป็นเมทริกซ์ได้ดังนี้

                 ดังนั้นจำนวนเงินที่ลดทั้งหมดของทั้งสองสาขาเป็นดังนี้
                                     
      
   =
   =
                                  

         
         จากผลลัพธ์ที่ได้แสดงว่า
                               สาขาที่ 1 จำนวนเงินที่ลด    แชมพู    1 ขวดเป็น  124 บาท
                                                                            สบู่         1 ขวดเป็น    36 บาท
                                                                           ยาย้อมผม 1 ขวดเป็น  334 บาท
                               สาขาที่ 2 จำนวนเงินที่ลด   แชมพู      1 ขวดเป็น    86 บาท
                                                                           สบู่           1 ขวดเป็น    29 บาท
                                                                          ยาย้อมผม  1 ขวดเป็น  226 บาท
                     ดีเทอร์มิแนนต์
               ดีเทอร์มิแนนต์ เป็นฟังก์ชันจานจำนวนจริงไปยังจำนวนจริง ซึ่งสัญลักษณ์ของงดีเทอมิแนนต์ แทนได้ 2 แบบคือให้คำว่า det
และใช้สัญลักษณ์ | |
               ใช้คำว่า det
        เป็นการใช้คำว่า det นำหน้าชื่อของเมทริกซ์ หรือ   นำหน้าเมทริกซ์ที่ประกอบด้วยสมาชิก

ตัวอย่าง 14  เป็นตัวอย่างของการใช้สัญลักษณ์คำว่า det แทนดีเทอร์มิแนนต์
                           ถ้าให้ A เป็นเมทริกซ์ ที่มีค่าเป็น
  A =
                                    
              ดังนั้นดีเทอร์มิแนนต์ของ A แทนเป็น
                           det A              เป็นการใช้ det นำหน้าชื่อเมทริกซ์
                                          หรือ
                         det( ) เป็นการใช้ det นำหน้าเมทริกซ์ที่ประกอบด้วยสมาชิกของ A

             ใช้สัญลักษณ์  |  |
    ที่ภายในสัญลักษณ์นี้ เป็นชื่อของเมทริกซ์หรือสมาชิกของเมทริกซ์

ตัวอย่าง 15 ถ้าให้ A เป็นเมทริกซ์ ที่มีค่าเป็น                  
  A =

                          

                    ดังนั้นดีเทอร์มิแนนต์ของ A แทนเป็น
                      | A |   เป็นการใช้สัญลักษณ์ |  |  ที่ภายในสัญลักษณ์เป็น    ชื่อของเมทริกซ์ ในที่นี้คือ A 
 หรือ
      | A |  =

                               
เป็นการใช้สัญลักษณ์ภายในสัญลักษณ์นี้เป็นสมาชิกของเมทริกซ์ ในที่นี้คือ     -3  3   2
                                                                                                                           -8  4   5
                                                                                                                           6  7  -1
วิธีการหาดีเทอร์มิแนนต์
              ในที่นี้จะใช้การพิจารณาจากมิติของเมทริกซ์จัตุรัสในการเลือกวิธีการใช้ในการหาค่าของดีเทอร์มิแนนต์
โดยจะกล่าวถึงการหาสำหรับเมทริกซ์ 2x2 ขึ้นไป
             เมทริกซ์มิติ  2x2
                      สำหรับเมทริกซ์มิติ 2x2 ในที่นี้ขอแนะนำให้ใช้สูตรในการหาค่าของดีเทอร์มิแนนต์ดังนี้
 
           ให้ A = 

                  
   ดังนั้น  
                                det A  = ad-bc          เมื่อ a, b, c, d เป็นจำนวนจริง


       
                



0 ความคิดเห็น:

สมัครสมาชิก: ส่งความคิดเห็น (Atom)